LeetCode 刷题大全

Hash Map

Leetcode41. 缺失的第一个正数

给定一个未排序的整数数组，找出其中没有出现的最小的正整数。

示例 1:

输入: [1,2,0]
输出: 3

示例 2:

输入: [3,4,-1,1]
输出: 2

示例 3:

输入: [7,8,9,11,12]
输出: 1

说明:

你的算法的时间复杂度应为O(n)，并且只能使用常数级别的空间。

搬运大佬的题解、我也是通过大佬的题解来写的。主要是n个数最多有1~n个数填充在里面，这点没有想到。

遍历一次数组把大于等于1的和小于数组大小的值放到原数组对应位置，然后再遍历一次数组查当前下标是否和值对应，如果不对应那这个下标就是答案，否则遍历完都没出现那么答案就是数组长度加1。

贴代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
 int firstMissingPositive(vector<int>& nums) {
        if(nums.size()==0)
        return 1;
        if(nums.size()==1)
        {
            if(nums[0]<1)
              return 1;
            else if(nums[0]==1)
              return 2;
            else
              return 1;
        }
  int n = nums.size();
  for (int i = 0; i < n; i++)
  {
	  while (nums[i] >= 1 && nums[i] <= n&&nums[i]!=i+1)
	  {
                if(nums[i]==nums[nums[i] - 1])
                  break;
		  swap(nums[i], nums[nums[i] - 1]);
	  }
  }
  for (int i = 0; i < n; i++)
  {
	  if (nums[i] != i + 1)
		  return i + 1;
  }
        return n+1;
 }
};

动态规划

leetcode32最长有效括号

给定一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: “(()”
输出: 2
解释: 最长有效括号子串为 “()”

示例 2:

输入: “)()())”
输出: 4
解释: 最长有效括号子串为 “()()”

​ 这题思路很清晰、用dp和stack记录括号的状态。dp数组记录当前连续括号对的个数。

( ) ( ( )
0 1 0 0 1

​ 当栈为空的时候，不再压入)。当遇到)时首先可以将这个位置执行dp[i]=dp[i-1]+1,因为这里和之前的一定是连续的，并且此时的dp值等于括号的对数，为了查看此时是否与之前的是连续括号对，可以查看i-dp[i]*2查看这个值是否大于零，大于零，则说明那处是一个括号对。

​ 代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
	int longestValidParentheses(string s) {
        if(s.length()==0)
            return 0;
		stack<char>sta;
		vector<int>dp(s.length(), 0);
		int i = 0;
		for (auto a:s)
		{
			if (a == '(')
				sta.push(a);
			else
			{
				if (sta.empty())
				{
					i++;
					continue;
				}
				dp[i] = dp[i - 1] + 1;
				int idx = dp[i] * 2;
				sta.pop();
				if (i - idx < 0)
				{
					i++;
					continue;
				}
				if (dp[i - idx] > 0)
					dp[i] += dp[i - idx];
			}
			i++;
		}

		int res = *max_element(dp.begin(), dp.end());
		return res*2;
	}
};

​ 这题用dp思路还是明确的。

956. 最高的广告牌

你正在安装一个广告牌，并希望它高度最大。这块广告牌将有两个钢制支架，两边各一个。每个钢支架的高度必须相等。

你有一堆可以焊接在一起的钢筋 rods。举个例子，如果钢筋的长度为 1、2 和 3，则可以将它们焊接在一起形成长度为 6 的支架。

返回广告牌的最大可能安装高度。如果没法安装广告牌，请返回 0。

示例 1：

输入：[1,2,3,6]
输出：6
解释：我们有两个不相交的子集 {1,2,3} 和 {6}，它们具有相同的和 sum = 6。

示例 2：

输入：[1,2,3,4,5,6]
输出：10
解释：我们有两个不相交的子集 {2,3,5} 和 {4,6}，它们具有相同的和 sum = 10。

示例 3：

输入：[1,2]
输出：0
解释：没法安装广告牌，所以返回 0。

  1. 0 <= rods.length <= 20

  2. 1 <= rods[i] <= 1000

  3. 钢筋的长度总和最多为 5000

    本题若按暴力法求解那么每个钢筋有三种状态，不拿、放左边、放右边。时间复杂度为三的N次方。看下数

    据在5000以下，看下dp方法。但是此题的状态转移方程很复杂。

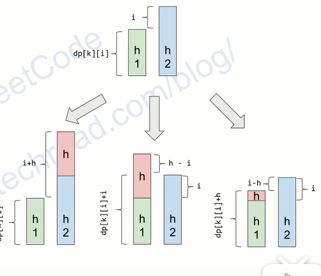
    s=dp[ i ] [j]表示前i个钢筋在相差j的时候的最大公共长度s。那么我们会有如下的转移方程。
    $$
    dp[n][i+h]=max(dp[n][i+h],dp[n-1][i])\
    dp[n][|i-h|]=max(dp[n][|i-h|],dp[n-1][i]+min(i,h))
    $$
    这个转移方程是很显然的，因为来一个钢筋只会出现这几种情况。最后放回dp[ n ] [0]即可

    考虑到可以用滚动数组，给出代码如下

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    class Solution {
     public:
    	 int tallestBillboard(vector<int>& rods) {
    		 int n = accumulate(rods.begin(), rods.end(), 0);
    		 vector<int>dp(n + 1, -1);
    		 dp[0] = 0;
    		 for (int gangjing : rods)
    		 {
    			 vector<int>cur(dp);
    			 for (int j = 0; j <= n - gangjing; j++)
    			 {
    				 if (cur[j] < 0)
    					 continue;

    				 dp[j + gangjing] = max(dp[j+gangjing],cur[j]);
    				 dp[abs(j - gangjing)] = max(dp[abs(j - gangjing)], cur[j] + min(gangjing, j));
    			 }
    		 }
    		 return dp[0];
    	 }
     };

664. 奇怪的打印机

有台奇怪的打印机有以下两个特殊要求：

打印机每次只能打印同一个字符序列。
每次可以在任意起始和结束位置打印新字符，并且会覆盖掉原来已有的字符。

给定一个只包含小写英文字母的字符串，你的任务是计算这个打印机打印它需要的最少次数。

示例 1:

输入: “aaabbb”
输出: 2
解释: 首先打印 “aaa” 然后打印 “bbb”。

示例 2:

输入: “aba”
输出: 2
解释: 首先打印 “aaa” 然后在第二个位置打印 “b” 覆盖掉原来的字符 ‘a’。

提示: 输入字符串的长度不会超过 100。

​ 长度不超过100，可以想到使用二维dp作dp

抄了别人的状态转移方程：
$$
s[i][i]=1 \
s[i][j]=\mathop{max}{k=1….j-1}(s[i][k]+s[k+1][j])-1\ \ if\ char[k]==char[j]\
s[i][j]=\mathop{max}{k=1….j-1}(s[i][k]+s[k+1][j])\ \ if\ char[k]!=char[j]
$$

我们的初始值就是s[ i ] [ i ]=1，没啥说的 直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
 int strangePrinter(string s) {
	 if (s.length() == 0)
		 return 0;
	 int n = s.length();
	 vector<vector<int>>dp(s.length(), vector<int>(s.length(), -1));
	 for (int i = 0; i < n; i++)
		 dp[i][i] = 1;
	 for (int i = 1; i < n; i++)
	 {
		 for (int j = 0; i + j < n; j++)
		 {
			 dp[j][i + j] = i + 1;
			 for (int k = j; k < i + j; k++)
			 {
				 if (s[k] == s[i + j])
					 dp[j][i + j] = min(dp[j][k] + dp[k + 1][i + j] - 1, dp[j][i + j]);
				 else
					 dp[j][i + j] = min(dp[j][k] + dp[k + 1][i + j], dp[j][i + j]);
			 }
		 }
	 }
	 return dp[0][n - 1];
 }
};

790. 多米诺和托米诺平铺

有两种形状的瓷砖：一种是 2x1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

XX <- 多米诺

XX <- “L” 托米诺
X

给定 N 的值，有多少种方法可以平铺 2 x N 的面板？返回值 mod 10^9 + 7。

（平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。）

示例:
输入: 3
输出: 5
解释:
下面列出了五种不同的方法，不同字母代表不同瓷砖：
XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY

​ 思路：根据花花的讲解，附上两张图就可以了，老规矩不总街了。

先从最简单的只有一个长方形的砖块看起。

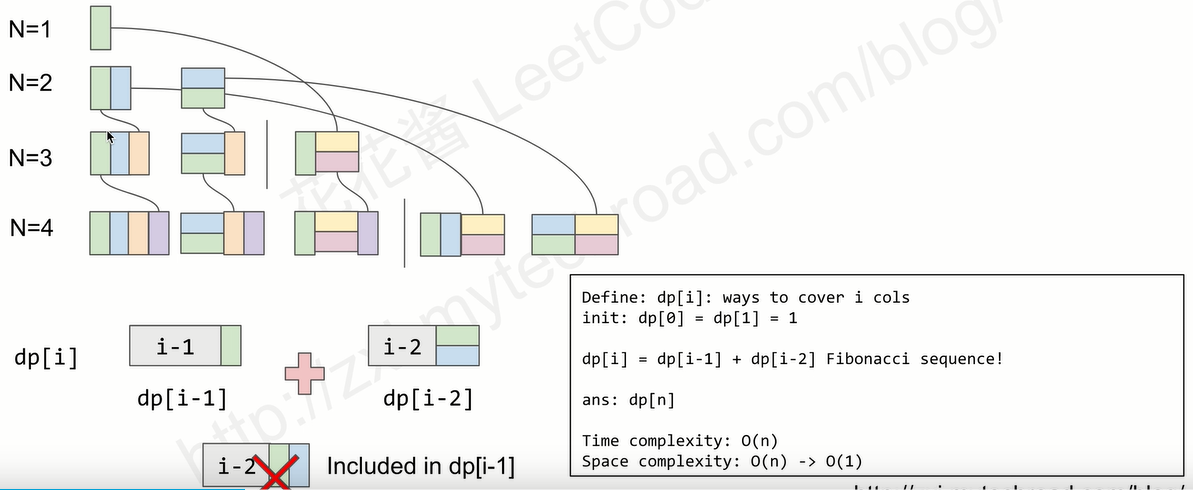
上述迭代公式是一个斐波拉且数列。再看看本题的转移方程。

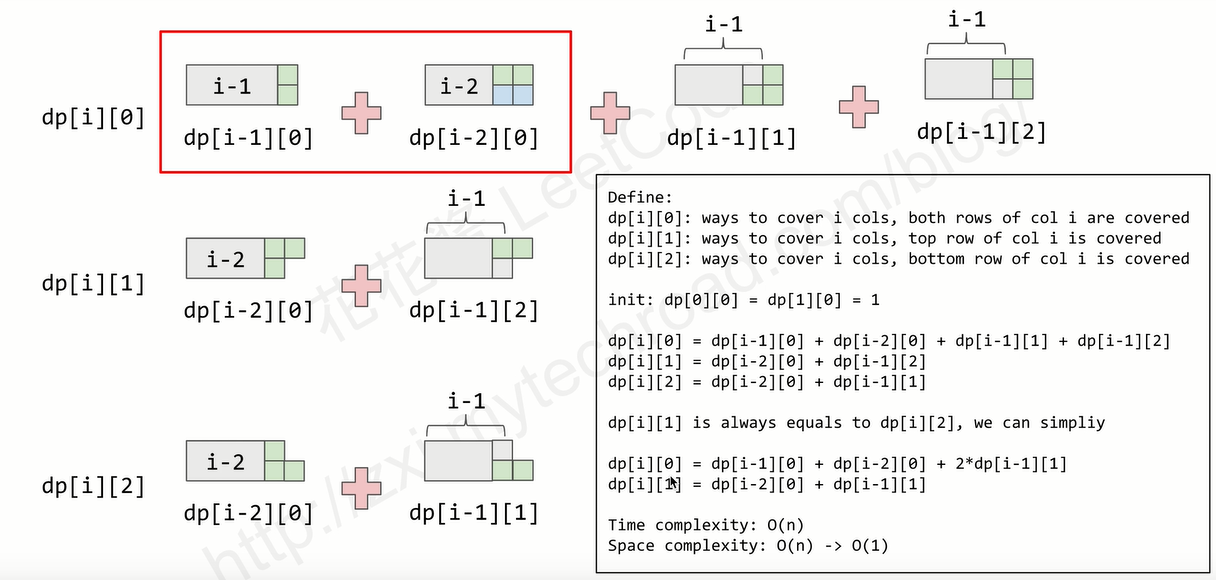
值得注意的是，图上有三个状态，但是状态二和状态三的数量相等，所以就省略了一个状态的状态转移方程，同时将dp【i】【0】-…..2*dp【i=1】【1】.

附上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
 int numTilings(int N) {
	 long mod = pow(10, 9) + 7;
	 vector<vector<long>>dp(N+1, vector<long>(2, 0));
	 dp[0][0] = dp[1][0] = 1;
	 for (int i = 2; i <= N; i++)
	 {
		 dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + 2 * dp[i - 1][1]) % mod;
		 dp[i][1] = (dp[i - 1][1] + dp[i - 2][0]) % mod;
	 }
	 return dp[N][0];
 }
};

72. 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1:

输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2:

输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

(抄别人的评论、自己写的太烂了)

  • 问题1：如果 word1[0..i-1] 到 word2[0..j-1] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换需要几步呢？
  • 答：先使用 k 步，把 word1[0..i-1] 变换到 word2[0..j-1]，消耗 k 步。再把 word1[i] 改成 word2[j]，就行了。如果 word1[i] == word2[j]，什么也不用做，一共消耗 k 步，否则需要修改，一共消耗 k + 1 步。
  • 问题2：如果 word1[0..i-1] 到 word2[0..j] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换需要消耗几步呢？
  • 答：先经过 k 步，把 word1[0..i-1] 变换到 word2[0..j]，消耗掉 k 步，再把 word1[i] 删除，这样，word1[0..i] 就完全变成了 word2[0..j] 了。一共 k + 1 步。
  • 问题3：如果 word1[0..i] 到 word2[0..j-1] 的变换需要消耗 k 步，那 word1[0..i] 到 word2[0..j] 的变换需要消耗几步呢？
  • 答：先经过 k 步，把 word1[0..i] 变换成 word2[0..j-1]，消耗掉 k 步，接下来，再插入一个字符 word2[j], word1[0..i] 就完全变成了 word2[0..j] 了。

从上面三个问题来看，word1[0..i] 变换成 word2[0..j] 主要有三种手段，用哪个消耗少，就用哪个。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
 int minDistance(string word1, string word2) {
	 int m = word1.length();
	 int n = word2.length();
	 vector<vector<int>>dp(m + 1, vector<int>(n + 1, 0));
	 for (int i = 0; i <= m; i++)
		 dp[i][0] = i;
	 for (int i = 0; i <= n; i++)
		 dp[0][i] = i;
	 for (int i = 1; i <= m; i++)
	 {
		 for (int j = 1; j <= n; j++)
		 {
			 if (word1[i - 1] == word2[j - 1])
				 dp[i][j] = dp[i - 1][j - 1];
			 else
				 dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]), dp[i][j - 1])+1;
		 }
	 }
	 return dp[m][n];
 }
};

712. 两个字符串的最小ASCII删除和

给定两个字符串s1, s2，找到使两个字符串相等所需删除字符的ASCII值的最小和。

示例 1:

输入: s1 = “sea”, s2 = “eat”
输出: 231
解释: 在 “sea” 中删除 “s” 并将 “s” 的值(115)加入总和。
在 “eat” 中删除 “t” 并将 116 加入总和。
结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例 2:

输入: s1 = “delete”, s2 = “leet”
输出: 403
解释: 在 “delete” 中删除 “dee” 字符串变成 “let”，
将 100[d]+101[e]+101[e] 加入总和。在 “leet” 中删除 “e” 将 101[e] 加入总和。
结束时，两个字符串都等于 “let”，结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 “lee” 或 “eet”，我们会得到 433 或 417 的结果，比答案更大。

注意:

0 < s1.length, s2.length <= 1000。
所有字符串中的字符ASCII值在[97, 122]之间。

​ 解法:同上题一样的解法; 状态分为最后一个字符相同与不相同的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
 int minimumDeleteSum(string s1, string s2) {
	 int m = s1.length(), n = s2.length();
	 vector<vector<int>>dp(m + 1, vector<int>(n + 1, 0));
	 for (int i = 1; i <= m; i++)
		 dp[i][0] = s1[i - 1] + dp[i - 1][0];
	 for (int j = 1; j <= n; j++)
		 dp[0][j] = dp[0][j - 1] + s2[j - 1];
	 for (int i = 1; i <= m; i++)
	 {
		 for (int j = 1; j <= n; j++)
		 {
			 if (s1[i - 1] == s2[j - 1])
				 dp[i][j] = dp[i - 1][j - 1];
			 else
			 {
				 dp[i][j] = min(min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]), dp[i - 1][j - 1] + s1[i - 1] + s2[j - 1]);
			 }
		 }
	 }
	 return dp[m][n];
 }
};

312. 戳气球

典型的区间型dp

有 n 个气球，编号为0 到 n-1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。每当你戳破一个气球 i 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。

求所能获得硬币的最大数量。

说明:

你可以假设 nums[-1] = nums[n] = 1，但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

示例:

输入: [3,1,5,8]
输出: 167
解释: nums = [3,1,5,8] –> [3,5,8] –> [3,8] –> [8] –> []
coins = 315 + 358 + 138 + 181 = 167

解答：与矩阵连乘的方法类似。考虑到边界的问题，将首位各自添加一个假的气球。nums.push_back(1); nums.insert(nums.begin(), 1); 这样即使是边界的气球也可以直接三个数相乘。将dp[i][j]定义为从第i个气球到第j个气球所能获得的最大收益，length从1开始到n，left从1开始，每次从left到right中间选择一个进行划分。（不能从中间到两边，因为搓破了中间的气球，再搓破两边的气球，这时两边的气球的分数彼此依赖。两边的气球就不再独立）每次选取最大值。代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
 int maxCoins(vector<int>& nums) {
	 int n = nums.size();
	 vector<vector<int>>dp(n + 2, vector<int>(n + 2, 0));
	 nums.push_back(1);
	 nums.insert(nums.begin(), 1);
	 for (int len = 1; len <= n; len++)
	 {
		 for (int left = 1; left <= n - len + 1; left++)
		 {
			 int right = left + len - 1;
			 for (int k = left; k <= right; k++)
			 {
				 int coin = nums[k] * nums[left - 1] * nums[right + 1];
				 dp[left][right] = max(dp[left][right], coin + dp[left][k - 1] + dp[k + 1][right]);
			 }
		 }
	 }
	 return dp[1][n];
 }
};

二分

二分普通模板

1
2
3
4
5
6
7
8
9
int l = 0, r = nums.size() - 1;
while (l < r)
{
 int mid = l + (r - l) / 2;
 if (nums[mid] >= target)
  r = mid;
 else
  l = mid + 1;
}

​ return的时候只用l的值具体的情况看具体的题目。注意找左端点的时候、右侧逼近、找右端点的时候左侧逼近。

​ 再来一个普遍的二分的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
int l=0,r=一个数;
int ans=0;
while(l<r)
{
	int mid=l+(r-l)/2;
	if(guss(条件))//guss函数为判定mid有效的函数
	{
		ans=L;
		L=mid+1;
	}
	else
	R=mid;
}

当然上述代码的L=mid+1与R=mid可以交换位置。最关键的就是设置guss函数

34. 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

​ 典型的二分细节的题目、先二分找左边的端点、在二分找右边的端点。细节见代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
 public:
  vector<int> searchRange(vector<int>& nums, int target) {
	  vector<int>res(2, -1);
         if(nums.size()==0)
           return res;
	  int l = 0, r = nums.size() - 1;
	  while (l < r)
	  {
		  int mid = l + (r - l) / 2;
		  if (nums[mid] >= target)//此处的大于等于就是当等于的时候右侧逼近
			  r = mid;
		  else
			  l = mid + 1;
	  }
	  if (nums[l] != target)
		  return res;
	  res[0] = l;
	  r = nums.size();//注意、找右侧端点的时候一般要将右侧的搜索范围加一
	  while (l < r)
	  {
		  int mid = l + (r - l) / 2;
		  if (nums[mid] > target)
			  r = mid;
		  else
			  l = mid + 1;
	  }
	  res[1] = l-1;//右侧的搜索范围加一以后，应该在返回的l减去一
	  return res;
  }
 };

410. 分割数组的最大值

给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。

注意:
数组长度 n 满足以下条件:

1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)

示例:

输入:
nums = [7,2,5,10,8]
m = 2

输出:
18

解释:
一共有四种方法将nums分割为2个子数组。
其中最好的方式是将其分为[7,2,5] 和 [10,8]，
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

​ 步骤： 分组的组数为m，最后输出的结果为y。很明显m与y成反比。例如m为数组长度，则y为数组的最大值。当m为1时，y为数组之和。所以可以使用二分法，下界是数组的最大值，上届是数组之和。然后guss函数满足一个贪心性质（见代码）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    
    //使用贪心算法，转换原题目的问题。二分法假定 mid是最大值，求m的数值
    public boolean guess(long mid,int [] nums, int m){
        long sum = 0;
        for(int i = 0; i < nums.length; i++){
            //当分隔的一边的和 大于最大值mid时， m --
            if(sum + nums[i] > mid){
                m --;
                sum = nums[i];
                //当数值的某个元素本身的值已经大于mid，说明假定mid最大值是错的，直接返回false，开始下一轮循环
                if(nums[i] > mid){
                    return false;
                }
            }else{
                sum += nums[i];
            }
        }
        return m >= 1;
    }
    public int splitArray(int[] nums, int m) {
        long L = 0, R = 1; //为了使用左开右闭，所以把右边界初始化为1
        long ans = 0;
        //确定二分法的左右边界，这里我用 左开右闭 即[0, sum + 1) ,
        for(int i = 0; i < nums.length; i ++){
            R += nums[i];
        }
        //二分法的套路
        //通过分析可以知道，当m越大，所求最大值会越小，即 m 与最大值呈现的是单调递减的关系
        while(L < R){
            long mid = (L + R) / 2;
            //判断为true时，由于是单调递减，需要把右边界左移
            if(guess(mid,nums,m)){
                ans = mid;
                R = mid;
            } else{
                L = mid + 1;
            }
        }
        return (int) ans;
    }
}

单调栈

456. 132模式

给定一个整数序列：a1, a2, …, an，一个132模式的子序列 ai, aj, ak 被定义为：当 i < j < k 时，ai < ak < aj。设计一个算法，当给定有 n 个数字的序列时，验证这个序列中是否含有132模式的子序列。

注意：n 的值小于15000。

示例1:

输入: [1, 2, 3, 4]

输出: False

解释: 序列中不存在132模式的子序列。

示例 2:

输入: [3, 1, 4, 2]

输出: True

解释: 序列中有 1 个132模式的子序列： [1, 4, 2].

示例 3:

输入: [-1, 3, 2, 0]

输出: True

解释: 序列中有 3 个132模式的的子序列: [-1, 3, 2], [-1, 3, 0] 和 [-1, 2, 0].

​ 最开始用暴力法，On的三次方，超时。用固定一个最小值的方法做。可以降维成On的平方。这里我们固定最小值，用nums[i]代表132中的3，nums[j]代表132中的2.当nums[i]为最小值的时候continue，因为nums[i]一定要大于最小值。

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
 bool find132pattern(vector<int>& nums) {
  int MIN = INT_MAX;
  for (int i = 0; i < nums.size(); i++)
  {
	  MIN = min(MIN, nums[i]);
	  if (MIN == nums[i])
		  continue;
	  for (int j = nums.size() - 1; j > i; j--)
	  {
		  if (nums[j]<nums[i] && nums[j]>MIN)
			  return true;
	  }
  }
  return false;
 }
};

​ 当然还有另外的解法，我们维持一个单调栈，思路是我们维护一个栈和一个变量 third，其中 third 就是第三个数字，也是 pattern 132 中的2，初始化为整型最小值，栈里面按顺序放所有大于 third 的数字，也是 pattern 132 中的3，那么我们在遍历的时候，如果当前数字小于 third，即 pattern 132 中的1找到了，我们直接返回 true 即可，因为已经找到了，注意我们应该从后往前遍历数组。如果当前数字大于栈顶元素，那么我们将栈顶数字取出，赋值给 third，然后将该数字压入栈，这样保证了栈里的元素仍然都是大于 third 的，我们想要的顺序依旧存在，进一步来说，栈里存放的都是可以维持坐标 second > third 的 second 值，其中的任何一个值都是大于当前的 third 值，如果有更大的值进来，那就等于形成了一个更优的 second > third 的这样一个组合，并且这时弹出的 third 值比以前的 third 值更大，为什么要保证 third 值更大，因为这样才可以更容易的满足当前的值 first 比 third 值小这个条件，举个例子来说吧，比如 [2, 4, 2, 3, 5]，由于是从后往前遍历，所以后三个数都不会进入 while 循环，那么栈中的数字为 5, 3, 2（其中2为栈顶元素），此时 third 还是整型最小，那么当遍历到4的时候，终于4大于栈顶元素2了，那么 third 赋值为2，且2出栈。此时继续 while 循环，因为4还是大于新栈顶元素3，此时 third 赋值为3，且3出栈。现在栈顶元素是5，那么 while 循环结束，将4压入栈。下一个数字2，小于 third，则找到符合要求的序列 [2, 4, 3]，参见代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
 bool find132pattern(vector<int>& nums) {
  int two = INT_MIN;
  stack<int>s;
  for (int i = nums.size() - 1; i >= 0; i--)
  {
	  if (nums[i] < two)
		  return true;
	  while (!s.empty() && nums[i] > s.top())
	  {
		  two = s.top(); s.pop();
	  }
	  s.push(nums[i]);
  }
  return false;
 }
};

数论

738. 单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

输入: N = 10
输出: 9

示例 2:

输入: N = 1234
输出: 1234

示例 3:

输入: N = 332
输出: 299

说明: N 是在 [0, 10^9] 范围内的一个整数。

​ 题解：先将数字变为字符串。若后一项比前一项小，则可以将前一项-1，然后把后面的项全部变为9，找到最前面的这个数字，直到真个字符串满足条件。见代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
 bool cheak(string s)
 {
	 for (int i = 0; i < s.length() - 1; i++)
		 if (s[i] > s[i + 1])
			 return false;
	 return true;
 }
 int monotoneIncreasingDigits(int N) {
	string s = to_string(N);
	int p=s.length();
	while (!cheak(s))
	{
		for (int i = s.length() - 1; i > 0; i--)
		{
			if (s[i] < s[i - 1])
			{
				string temp = s.substr(0, i );
				int shu = stoi(temp);
				shu -= 1;
				p = i;
				s = to_string(shu) + s.substr(i, s.length()-i+1);
			}
		}
		for (int i = p; i < s.length(); i++)
			s[i] = '9';
	}
	return stoi(s);

 }
};

含有循环性质的解法

957. N 天后的牢房

8 间牢房排成一排，每间牢房不是有人住就是空着。

每天，无论牢房是被占用或空置，都会根据以下规则进行更改：

如果一间牢房的两个相邻的房间都被占用或都是空的，那么该牢房就会被占用。
否则，它就会被空置。

（请注意，由于监狱中的牢房排成一行，所以行中的第一个和最后一个房间无法有两个相邻的房间。）

我们用以下方式描述监狱的当前状态：如果第 i 间牢房被占用，则 cell[i]==1，否则 cell[i]==0。

根据监狱的初始状态，在 N 天后返回监狱的状况（和上述 N 种变化）。

示例 1：

输入：cells = [0,1,0,1,1,0,0,1], N = 7
输出：[0,0,1,1,0,0,0,0]
解释：
下表概述了监狱每天的状况：
Day 0: [0, 1, 0, 1, 1, 0, 0, 1]
Day 1: [0, 1, 1, 0, 0, 0, 0, 0]
Day 2: [0, 0, 0, 0, 1, 1, 1, 0]
Day 3: [0, 1, 1, 0, 0, 1, 0, 0]
Day 4: [0, 0, 0, 0, 0, 1, 0, 0]
Day 5: [0, 1, 1, 1, 0, 1, 0, 0]
Day 6: [0, 0, 1, 0, 1, 1, 0, 0]
Day 7: [0, 0, 1, 1, 0, 0, 0, 0]

示例 2：

输入：cells = [1,0,0,1,0,0,1,0], N = 1000000000
输出：[0,0,1,1,1,1,1,0]

提示：

cells.length == 8
cells[i] 的值为 0 或 1 
1 <= N <= 10^9

​ 题解: 很明显总共有二的八次方256种状态，那么状态肯定存在循环。可以使用一个map来记录这些状态。找到合适的记录状态的方法，例如磁体我们可以采用int 对 int 的map，键为次数，值为位数+二的位数次方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
 vector<int> prisonAfterNDays(vector<int>& cells, int N) {
	 unordered_map<int, int> intMap;
	 vector<int> tmp(8, 0);
	 int i = 1;
	 while (i <= N) {
		 for (int i = 1; i < 7; i++) {
			 tmp[i] = (cells[i - 1] == cells[i + 1]);
		 }
		 tmp[0] = 0; tmp[7] = 0;
		 swap(tmp, cells);

		 // judge
		 int val = 0;
		 for (int i = 0; i < 7; i++) val = val * 2 + cells[i];
		 if (intMap.find(val) == intMap.end()) {
			 intMap[val] = i;
		 }
		 else {
			 // 出现重复,计算res
			 int cycle_len = i - intMap[val];
			 i = i + (N - i) / cycle_len*cycle_len;
		 }
		 i++;
	 }

	 return cells;
 }
};

DFS

124. 二叉树中的最大路径和

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

  1
 / \
2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

-10
/
9 20
/
15 7

输出: 42

​ 这种题直接上代码把，我觉得我也说不秦楚。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
 int res = INT_MIN;
 int fun(TreeNode* root)
 {
	 if (root == nullptr)
		 return 0;
	 int left = max(fun(root->left), 0);
	 int right = max(fun(root->right), 0);
	 res = max(res, root->val + left + right);
	 return max(left, right) + root->val;
 }
 int maxPathSum(TreeNode* root) {
	 fun(root);
	 return res;
 }
};

回溯剪枝

79. 单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
[‘A’,’B’,’C’,’E’],
[‘S’,’F’,’C’,’S’],
[‘A’,’D’,’E’,’E’]
]

给定 word = “ABCCED”, 返回 true.
给定 word = “SEE”, 返回 true.
给定 word = “ABCB”, 返回 false.

​ 典型的深搜剪枝的题目，不过这题传参的时候多传递一个用于表示该位置是否搜索过的数组。当然也可以使用全局的数组来表示。直接上代码，比较简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
	bool dfs(vector<vector<char>>& board, string& word, int num, int x, int y,vector<vector<int>>&f)
	{
		if (num == word.size())
			return true;
		if (x < 0 || x >= board.size() || y < 0 || y >= board[0].size()||board[x][y]!=word[num])
			return false;
		if (f[x][y] == 0)
		{
			f[x][y] = 1;
			if (dfs(board, word, num + 1, x + 1, y, f) || dfs(board, word, num + 1, x - 1, y, f) || dfs(board, word, num + 1, x, y + 1, f) || dfs(board, word, num + 1, x, y - 1, f))
				return true;
			f[x][y] = 0;
		}
		return false;
	}
	bool exist(vector<vector<char>>& board, string word) {
		if (board.empty() || word.empty())
			return false;
		int m = board.size(), n = board[0].size();
		vector<vector<int>> visit(m, vector<int>(n, 0));
		for (int i = 0; i < m; i++)
		{
			for (int j = 0; j < n; j++)
			{
				if (dfs(board, word, 0, i, j))
					return true;
			}
		}
		return false;
	}
};

37. 解数独

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 ‘.’ 表示。

一个数独。

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

​ 题解 深搜剪枝 ，细节较多而已，用三个二维数组分别存储行列块的位数信息，dfs采用控制三个数组来回溯，比用if语句控制回溯要好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
public:
 bool dfs(vector<vector<char>>&board, vector<vector<bool>>&col, vector<vector<bool>>&row, vector<vector<bool>>&block, int i, int j)
 {
  while (board[i][j] != '.')
  {
	  if (++j >= 9)
	  {
		  i++;
		  j = 0;
	  }
	  if (i >= 9)
	  {
		  return true;
	  }
  }
  for (int num = 1; num <= 9; num++)
  {
	  int bloIdex = i / 3 * 3 + j / 3;
	  if (!col[i][num] && !row[j][num] && !block[bloIdex][num])
	  {
		  col[i][num] = true;
		  row[j][num] = true;
		  block[bloIdex][num] = true;
		  board[i][j] = '0' + num;
		  if (dfs(board, col, row, block, i, j))
			  return true;
		  else
		  {
			  col[i][num] = false;
			  row[j][num] = false;
			  block[bloIdex][num] = false;
			  board[i][j] = '.';
		  }
	  }
  }
  return false;
 }

 void solveSudoku(vector<vector<char>>& board) {
  vector<vector<bool>>col(9, vector<bool>(10,false));
  vector<vector<bool>>row(9, vector<bool>(10, false));
  vector<vector<bool>>block(9, vector<bool>(10, false));
  for (int i = 0; i < 9; i++)
  {
	  for (int j = 0; j < 9; j++)
	  {
		  if(board[i][j]!='.')
		  {
			  int num = board[i][j] - '0';
			  col[i][num] = true;
			  row[j][num] = true;
			  block[i / 3 * 3 + j / 3][num] = true;
		  }
	  }
  }
  dfs(board, col, row, block, 0, 0);
 }
};

10. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例 1:

输入:
s = “aa”
p = “a”
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。

示例 2:

输入:
s = “aa”
p = “a“

输出: true
解释: 因为 ‘‘ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例 3:

输入:
s = “ab”
p = “.*”
输出: true
解释: “.*” 表示可匹配零个或多个（’*’）任意字符（’.’）。

示例 4:

输入:
s = “aab”
p = “cab”
输出: true
解释: 因为 ‘*’ 表示零个或多个，这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。

示例 5:

输入:
s = “mississippi”
p = “misis*p.”
输出: false

杂项

leetcode55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

步步为营。从后之前，从后往前遍历数组，如果遇到的元素可以到达最后一行，则截断后边的元素。否则继续往前，弱最后剩下的元素大于1个，则可以判断为假。否则就是真，时间复杂度O(n)就可以，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
 bool canJump(vector<int>& nums) {
  int n = 1;
  for (int i = nums.size() - 2; i >= 0; i--)
  {
	  if (nums[i] >= n)
	  {
		  n = 1;
	  }
	  else
		  n++;
	  if (i == 0 && n != 1)
	  {
		  return false;
	  }
  }
  return true;
 }
};

方法

  1. substr()第一个参数为起始的位置，第二个参数为字符串大小

  2. 使用to_string()化为string,stoi()化为int

  3. 见664奇怪的打印机，如果dp时求一轮1，2 2，3 3，4，二轮 1，3 2，4 时可以将外部循环设置为步长，内部为起始点。

  4. 图内的找点法、一列一列的找。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    while (board[i][j] != '.')
    		  {
    			  if (++j >= 9)
    			  {
    				  i++;
    				  j = 0;
    			  }
    			  if (i >= 9)
    			  {
    				  return true;
    			  }
    		  }

  5. 在C++（补码环境下）a&(-a)可以得到a的最低非零位

STL

优先队列–priority_queue

​ 使用优先队列必须包含头文件#include 

定义：priority_queue<Type, Container, Functional>

Type 就是数据类型，Container 就是容器类型（Container必须是用数组实现的容器，比如vector,deque等等，但不能用 list。STL里面默认用的是vector），Functional 就是比较的方式，当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆

//升序队列 priority_queue <int,vector,greater > q;

//降序队列 priority_queue <int,vector,less >q;

当然当元素为一个pair时我们可以根据第一个和第二个元素的性质来设置优先队列，方法如下

1
2
3
4
5
6
7
8
using D = pair<string,string>;
struct comp{
    bool operator()(D x, D y) {
        return x.second.size() < y.second.size();
    }
};
priority_queue<pair<string,string>,vector<pair<string,string>>,comp>d;
//这样就可以按照第二个元素升序的顺序出队列

和队列相同的操作

  • top 访问队头元素
  • empty 队列是否为空
  • size 返回队列内元素个数
  • push 插入元素到队尾 (并排序)
  • emplace 原地构造一个元素并插入队列
  • pop 弹出队头元素
  • swap 交换内容

数据结构

字典树

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家