线性分类的种类
按照分类的方式大致可以分为以下几类
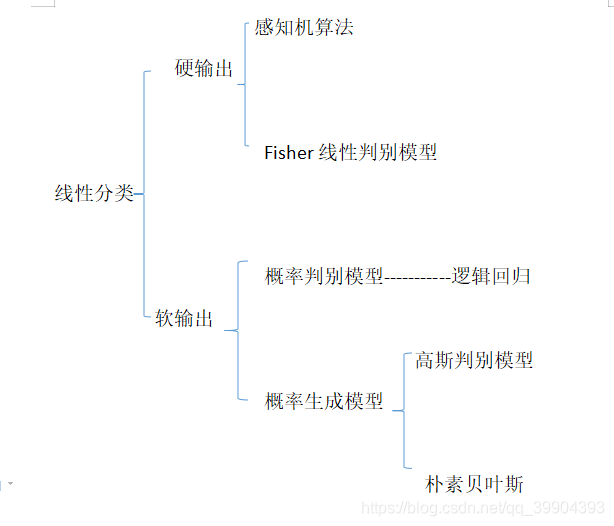
硬输出与软输出
硬输出顾名思义就是给定一个输入就有一个标签的输出值,而软输出会输出这个输入样本所属于这类标签的概率。
概率判别模型与概率生成模型
概率判别模型
例如逻辑回归,给定一个sigmoid函数,计算p(y|x),判断计算的概率大于0.5还是下雨0.5
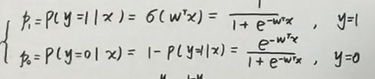
再通过极大似然估计计算所属的标签
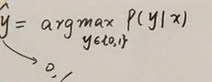
概率生成模型
概率生成模型不直接计算P(Y|X)而是借助了贝叶斯公式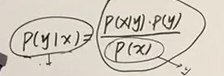
而计算的P(x)在每个计算过程中都是一致的,所以我们有了如下的似然函数
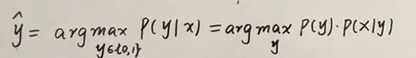
高斯判别模型
假设y服从二项分布
$$
y\sim B(\phi)
$$
X|Y服从正态分布
$$
X|Y=1\sim{N(\mu_1,\Sigma)}\
X|Y=0\sim{N(\mu_2,\Sigma)}
$$
对采样样本进行分类
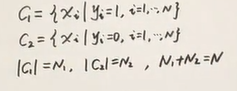 )(十四)
)(十四)
定义似然函数为
$$
L(\theta)=log\prod_{i=1}^NP(x_i,y_i)(六)
$$
则我们可以简化这个似然函数
$$
L(\theta)=\sum_{i=1}^Nlog(P(x_i|y_i)P(y_i))
$$
$$
=\sum_{i=1}^N[ log\ P(x_i|y_i)+log\ P(y_i)](六)
$$
这时候我们把Y和X|Y的分布写成一个式子,就有
$$
P(y=1或y=0)=\phi^y\phi^{1-y}
$$
$$
P(y=0|x或y=1|x)={N(\mu_0,\Sigma)}^yN(\mu_1,\Sigma)^{1-y}(七)
$$
将七式代入六式之中、有
$$
L( \theta ) = \sum_{i=1}^N(log\ N(\mu_1,\Sigma)^{y_i}+log\ N(\mu_2,\Sigma)^{1-y_i}+log\ \phi^{y_i}(1-\phi)^{1-y_i})(八)
$$
求高斯模型中的参数
> 后面的公式推导直接上图片了、打的太累了补充几个矩阵上的定理
 )(十)
)(十)
求phi
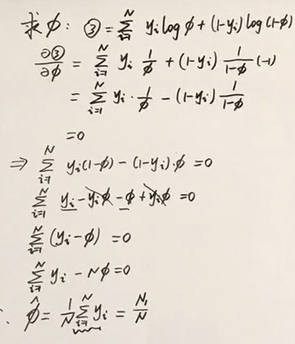 )(十一)
)(十一)
求u
 )(十二)
)(十二)
 )(十三)
)(十三)
令
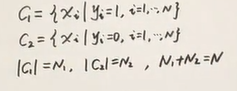 )(十五)
)(十五)
有
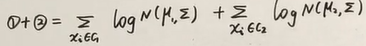 )(十六)
)(十六)
求sigma
 (十七)
(十七)
上式的左式的最后一项为一个常熟,考虑矩阵的tr(),和样本方差(我们定义的方差如下,不考虑无偏估计量)
$$
\sum_{i=1}^N\frac{(x_i-\mu)^T(x_i-\mu)}(十八)
$$
又由于tr(ABC)=tr(BCA)=tr(CAB),那么
十七公式可以计算成
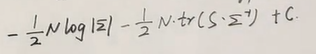 )(十九)
)(十九)
 )(二十)
)(二十)
这里写错了 N1那个S应该写成S1、N2的S应写成S2 因为是不同的样本的样本方差
这个时候在求导
 )(二十一)
)(二十一)
朴素贝叶斯分类器
朴素贝叶斯是基于概率论贝叶斯公式 来进行建模的。他的大致思路是先求出p(y)的先验概率,
$$
p(y|x)=\frac{p(y)*p(x|y)}{p(x)} (一)
$$
通过找到一个最大的标签yi,让下面这个式子最大
$$
\mathop{argmax}\limits_{y_{ck}\in{Y}}p(y_{ck}*p(x|y_{ck}))(二)
$$
频率派与贝叶斯派
频率派认为上述式子应该采用极大似然估计来估算yck,而贝叶斯派则认为参数yck应该服从某种分布,英雌可以根据某一种分布来估计鲜先验,然后再计算后验。本文采用频率派的观点,用极大似然估计计算yck
极大似然估计
假设公式(一)中的p(x|y)xixi相互独立 则下面式子成立,其中Dc为样本空间
$$
p(x|y_{ck})=\prod_{x\in{D_c}}p(x|y_{ck})(三)
$$
对yck进行似然估计,就是对yck在标签类中取值使得p(x|yck)最大,对上述式子取对数,有
$$
LL(y_{ck})=log\ P(D_c|y_{ck})
$$
$$
=\sum_{x\in{D_c}}log\ P(x|y_{ck})(四)
$$
我们要找到一个yck让LL(yck)最大,
朴素贝叶斯分类器
朴素贝叶斯分类器还有如下的假设,属性的假设相互独立^相互独立
有了上面的基础,那么我们可以把上面的公式重写为如下的公式五,其中d为标签的种类个数
$$
h_{nb}=\mathop{argmax}\limits_{y_{ck}\in{Y}}\ P(y_{ck})\prod_{i=1}^{d}P(x_{i}|y_{ck})(五)
$$
代入计算即可,具体的计算过程见西瓜书p151


