概率图模型基础

2019-10-28

概率图模型分类

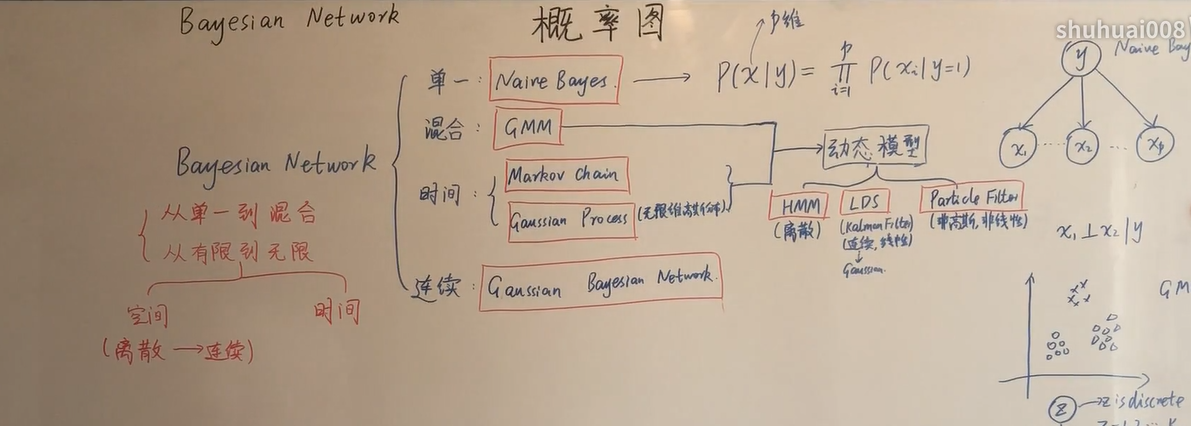
概率图模型的背景

高维随机变量的困境，维度越高，联合概率的计算量变大
$$
P(x_!,x_2,…,x_n)=\prod_{i=1}^n{p(x_i|x_1,x_2,…,x_{i-1})}（一）
$$
假设每个维度的随机变量的维度相互独立(朴素贝叶斯)，但是朴素贝叶斯这个假设比强强，我们放松成一阶齐次马尔可夫性质^马尔可夫。一阶其次马尔可夫假设条件也太高了，我们引出条件独立性假设[^条件独立性假设]

条件独立性假设可以简化公式一的链式过程

概率图模型的大致分类

概率图模型

贝叶斯网络表达条件独立性

tialtotial

假设贝叶斯网络长成这样

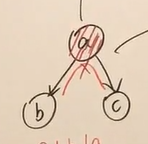
tialtotial

则我们称这个为tialtotial 型，其中给定的A下B与C独立
$$
B\perp{C}|A (二)
$$
推导如下
$$
由图可知\
P(a,b,c)=p(a)p(b|a)p(c|a)\
而\p(a,b,c)=p(a)p(b|a)p(c|(a,b))
\则\p(c|a)=p(c|(a,b))\
两边同时乘上p(b|a)有\
p(c|a)p(b|a)=p(c|(a,b))p(b|a)=p((b,c)|a)\
p(c|A)p(b|a)=p((b,c)|a)\Rightarrow{B\perp{C}|A}
$$

headtotial

假设贝叶斯网络长成这样

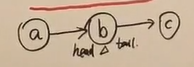
headtotial

则我们称这个为headtotial型，其中给定的B下A与C独立
$$
A\perp{C}|B (三)\
\ \
\ \
也就是说 p(abc)=p(a)p(b|a)p(c|b)
$$

headtohead

假设贝叶斯网络长成这样

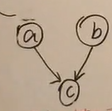
tialtotial

则此时默认情况下a,b独立，若C被观测则a,b不独立

解释一下headto head模型

如下面的贝叶斯网络

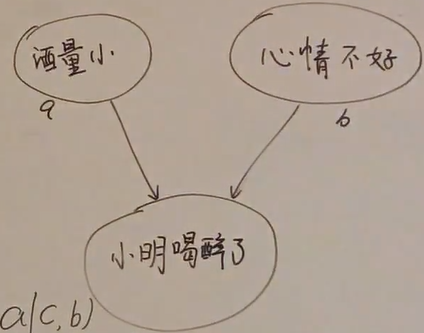
小明喝醉了

若小明喝醉了c没有发生，则酒量小a与心情不好b是独立的。一旦c发生，那么
$$
P(a|c)一定大于P(a|cb)
$$
因为心情不好和酒量小都影响这小明喝醉了，而当b心情不好也发生时，酒量小的概率就更加低了。

再解释一下headtohead模型

假如我们的概率图长成这个样子

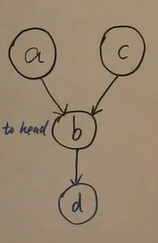
小明喝醉了2

如果此时d被观测，那么a与c也就不再独立，对应事件为

a: 小明酒量低
b: 小明心情不好
c: 小明喝醉了
d： 小明吐了

如果小明吐了发生了,那么此时小明酒量低和小明心情不好就不再独立了。

以上三种模型可以想象成白板推导的亲戚关系

所谓的被观测是指该事件要发生

Markov Network

无向概率图模型

gloab markov

$$
X_A\perp{X_c}|X_b\ \ 用无向图表示
$$

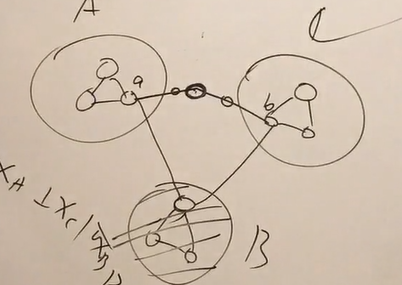
在全局马尔可夫里，A到C至少要经过B、这样当阻塞B时A与C独立

local markov

在local马尔可夫性里、在观测a的邻居是，a与其他节点独立

成对markov

不做过多的解释。

这三个马尔可夫性是可以相互证明的

因子分解

##### 团的定义

在一个无向图中，最大团的定义为连通分量

则我们定义的马尔可夫场的P（X）为
$$
P(x)=\frac{1}{Z}\prod_{i=1}^{k}\Psi(X_{C_i})
$$
其中
$$
Z=\sum_{x}\prod_{i=1}^{k}\Psi(X_{C_i})=\sum_{x_1}\sum_{x_2}…\sum_{x_p}\prod_{i=1}^{k}\Psi(X_{C_i})
$$
在上述公式中
$$
C_i表示最大团\
X_{C_i}表示最大团的变量集合\
\Psi(X_{C_i})为势函数\
p为x的维度
$$
势函数的定义为能量函数

EM算法

我们先写出theta的对数似然MLE
$$
\theta_{MLE}=\mathop{argmax}_{\theta}logP(x|\theta)（一）
$$

EM算法的公式

$$
\theta^{t+1}=\mathop{argmax}{\theta}\int{Z}log P(x,z|\theta)*p(z|x,\theta^{(t)})dz（二）
$$

其中EM算法的思路是让期望最大

其中
$$
\theta是模型的参数 \
z是隐变量
$$

因此在一式的每一次迭代中都有下一次的结果大于等于上一次的结果才可以、这个是我们运用一式后所能得到的结果、也就是
$$
logP(x|\theta^{t})\le{logP(x|\theta^{t+1})}(三)
$$

当theta 已知时